[ISNLP 오픈 튜토리얼] 1일차: 선형 회귀와 로지스틱 회귀 실습

게시 2025/06/23 업데이트 2025/08/28

ISNLP 1일차: 선형 회귀와 로지스틱 회귀

By 한재욱

4 분읽는 시간

[ISNLP 오픈 튜토리얼] 1일차: 선형 회귀와 로지스틱 회귀 실습

1일차: 선형 회귀 & 로지스틱 회귀 정리

운좋게도 가천대학교 자연어 처리 연구실 ISNLP에서 여름방학 동안 진행하는 자연어처리 오픈 튜토리얼에 선발되게 되었다. 배운 내용을 글로 정리해두면 좋을 것 같아서 간단하게라도 기록하기로 하였다.

1일차 수업에서는 머신러닝의 가장 기초적인 모델인
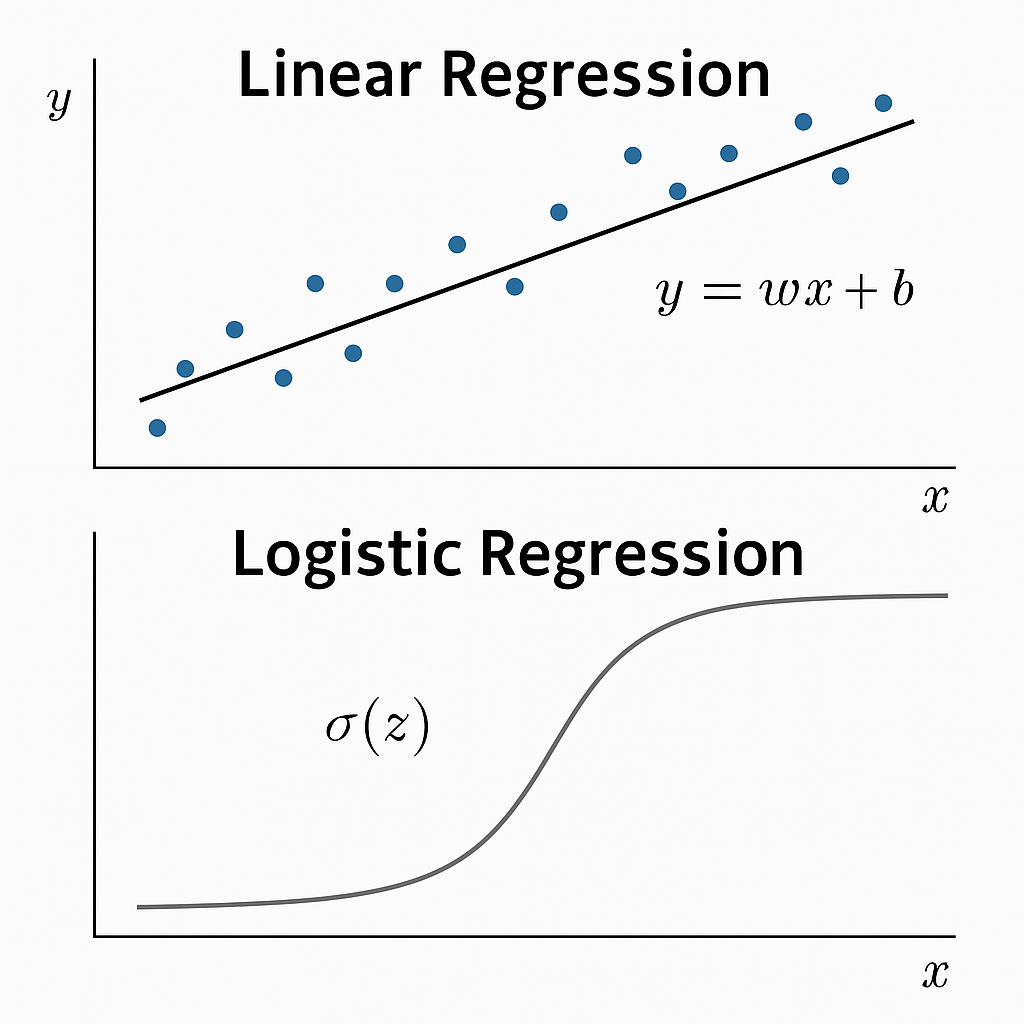
선형 회귀(Linear Regression)와 로지스틱 회귀(Logistic Regression)를 학습하고
직접 Python과 PyTorch로 구현해보았다.

이번 글에서는 내가 이해한 내용을 정리해본다.

1. 선형 회귀 (Linear Regression)

1-1. 핵심 개념

입력(feature)과 출력(label) 간의 선형 관계를 학습하는 모델
예측식:
\(\hat{y} = ax + b\)
손실 함수: MSE(Mean Squared Error)
\(MSE = \frac{1}{n} \sum_{i=1}^{n} (\hat{y_i} - y_i)^2\)

핵심 포인트:
데이터를 가장 잘 표현하는 직선을 찾는 문제
손실 함수 값이 작을수록 모델이 데이터를 잘 설명한다

1-2. 최소제곱법 (Least Squares)

MSE를 최소화하는 닫힌 형태의 해(closed-form)를 바로 구할 수 있음

  
import numpy as np

x = np.array([10, 15, 20, 25])
y = np.array([1, 2, 3, 4])

a = np.sum((x - x.mean())*(y - y.mean())) / np.sum((x-x.mean())**2)
b = y.mean() - a*x.mean()
print(f"직선 방정식: y = {a:.2f}x + {b:.2f}")

1-3. 경사 하강법 (Gradient Descent)

반복적으로 파라미터를 업데이트하여 MSE를 최소화하는 방법
업데이트 식: \(a \leftarrow a - \alpha \frac{\partial MSE}{\partial a}, \quad b \leftarrow b - \alpha \frac{\partial MSE}{\partial b}\)

  
learning_rate = 0.01
a, b = 0.0, 0.0

for epoch in range(100):
    y_pred = a*x + b
    grad_a = (-2/len(x)) * sum(x * (y - y_pred))
    grad_b = (-2/len(x)) * sum(y - y_pred)
    
    a -= learning_rate * grad_a
    b -= learning_rate * grad_b

2. 로지스틱 회귀 (Logistic Regression)

2-1. 핵심 개념

이진 분류(Binary Classification) 문제 해결용 모델
선형 회귀 결과를 Sigmoid 함수를 통해 확률로 변환 \(\sigma(z) = \frac{1}{1 + e^{-z}}\)
손실 함수: Binary Cross-Entropy \(L = -\frac{1}{n} \sum_{i=1}^{n} \big[ y_i \log \hat{y_i} + (1-y_i) \log(1-\hat{y_i}) \big]\)

핵심 포인트:
0과 1 사이의 확률을 출력
Cross-Entropy 손실을 최소화하며 학습

2-2. PyTorch 구현 실습

  
import torch

X = torch.tensor([[25, 12, 40]], dtype=torch.float32)
y = torch.tensor([1], dtype=torch.float32)

w = torch.randn((3,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

sigmoid = torch.nn.Sigmoid()
loss_fn = torch.nn.BCELoss()
optimizer = torch.optim.SGD([w,b], lr=0.01)

for epoch in range(100):
    y_pred = sigmoid(X @ w + b)
    loss = loss_fn(y_pred, y.unsqueeze(1))
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

3. 오늘 배운 내용 정리

3-1. 중요한 포인트

선형 회귀와 로지스틱 회귀의 차이는 출력 값과 손실 함수에서 나타난다.
경사 하강법을 직접 구현하면서 기울기(Gradient)와 학습률(Learning Rate)의 중요성을 체감.

3-2. 배운 점

수식을 직접 코드로 옮기면서 수식 → 미분 → 파라미터 업데이트 흐름을 명확히 이해했다.
PyTorch의 기초 학습 흐름(requires_grad, backward(), optimizer.step())을 익혔다.

3-3. 느낀 점

케라스/텐서플로우 위주로만 써왔는데 PyTorch의 구조를 이해할 수 있어 유익했다.
이미 알고 있다고 생각했던 내용도 직접 구현하니 확실히 복습할 수 있었고,
기초를 다지는 것의 중요성을 다시 한번 느낀 하루였다.

4. 참고 자료

다음 글에서는 2일차: MLP와 딥러닝 기초 내용을 정리할 예정이다.

ISNLP_Open_Tutorial, 학습일지